Many-body expansions#

The many-body expansion (MBE) represents the total system energy, \(E\), composed of \(N\) non-covalently connected (i.e., non-intersecting) fragments/monomers as the sum of \(n\)-body interaction energies:

(1)#\[E = \sum_{i}^N E_i^{(1)} + \sum_{i < j}^N \Delta E_{i,j}^{(2)} + \sum_{i < j < k}^N \Delta E_{i,j,k}^{(3)} + \cdots.\]

Here, \(N\) is the number of monomers; \(i\), \(j\), and \(k\) are monomer indices; \(E_i^{(1)}\) is the energy of monomer \(i\); and \(\Delta E_{\; i, \: j, \: \ldots}^{\; (n)}\) represents the \(n\)-body interaction energy contribution of the structure containing fragments \(i\), \(j\), \(\ldots\) with lower order (\(< n\)) contributions removed. For example, the 2-body contribution of \(i\) and \(j\) is

(2)#\[\Delta E_{i,j}^{(2)} = E_{i,j}^{(2)} - E_{i}^{(1)} - E_{j}^{(1)},\]

and the 3-body contributions with monomers \(i\), \(j\), and \(k\) are

(3)#\[\Delta E_{i,j,k}^{(3)} = E_{i,j,k}^{(3)} - \Delta E_{i,j}^{(2)} - \Delta E_{i,k}^{(2)} - \Delta E_{j,k}^{(2)} - E_{i}^{(1)} - E_{j}^{(1)} - E_{k}^{(1)}.\]

Equation (1) is exact when all \(n\)-body contributions up to \(N\) are accounted for with exact accuracy and precision. This equation also holds for properties that can be expressed as a derivative of energy (e.g., gradients). In practice, the expansion is always truncated to some order, \(n\), which is usually 3.

What is a fragment?#

MBEs are built upon what we define our fragments/monomers to be. A fragment is a group of atoms we represent as a monomer used to define \(n\)-body interactions. Procedures to fragment the system are classified based on two categories:

Covalent fragments#: Whether a fragment “breaks” covalent bonds. Non-covalent fragments occur when the entire molecule is its own fragment. Separating a molecule into individual fragments is possible, but there are additional complexities. Therefore, we do not consider covalent fragments here.
Intersecting fragments#: Nothing precludes defining fragments with more than one molecule. This changes the many-body formulation, and Equation (1) is not applicable. The principle of inclusion and exclusion (PIE) generally is used with intersecting fragments. We do not support this yet. Only non-intersecting fragments are considered here.

Non-covalent, non-intersecting fragments are the default in almost all of our cases.

The choice is yours, but the driving aspect of selecting a fragmentation scheme is often the number and size of \(n\)-body combinations. For example, if we consider a water trimer, there are substantially more 2- and 3-body structures if we fragment with respect to atoms instead of molecules. Not to mention that whole molecular fragments are typically more accurate. The computational cost of fragments also becomes an issue if they are particularly large.

See no free lunch for more discussion.

Water trimer example#

We find MBEs are much easier to understand with an example. Suppose we want to compute the energy of the following trimer with MP2/def2-TZVP and that this level of theory is intractable. This calculation is possible in a matter of seconds—as the energy is shown below—but imagine we cannot.

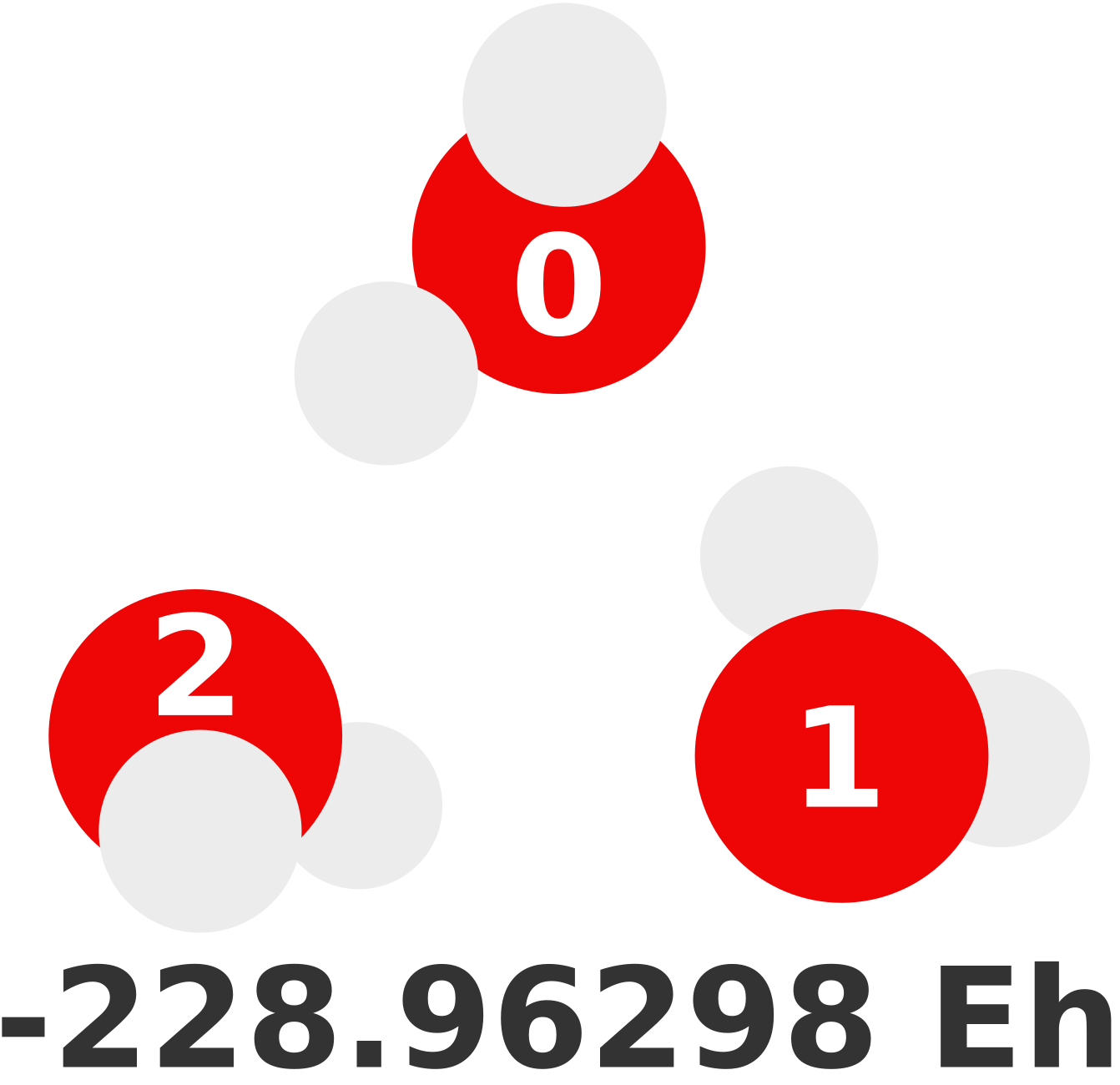
1-body#

The first term of the MBE (Equation (1)) represents the 1-body contributions of this structure. Before this, we must define our 1-body structures or fragments. Each molecule will be a fragment since they are small and it is a non-covalent cluster (fragment indices are shown above). Thus, our 1-body prediction, \(E^{(1)}\), of this trimer would be

\[E^{(1)} = E_0^{(1)} + E_1^{(1)} + E_2^{(1)}.\]

\(E_0^{(1)}\) means the total energy of monomer 0 calculated at our desired level of theory: MP2/def2-TZVP. Each monomer energy is shown below.

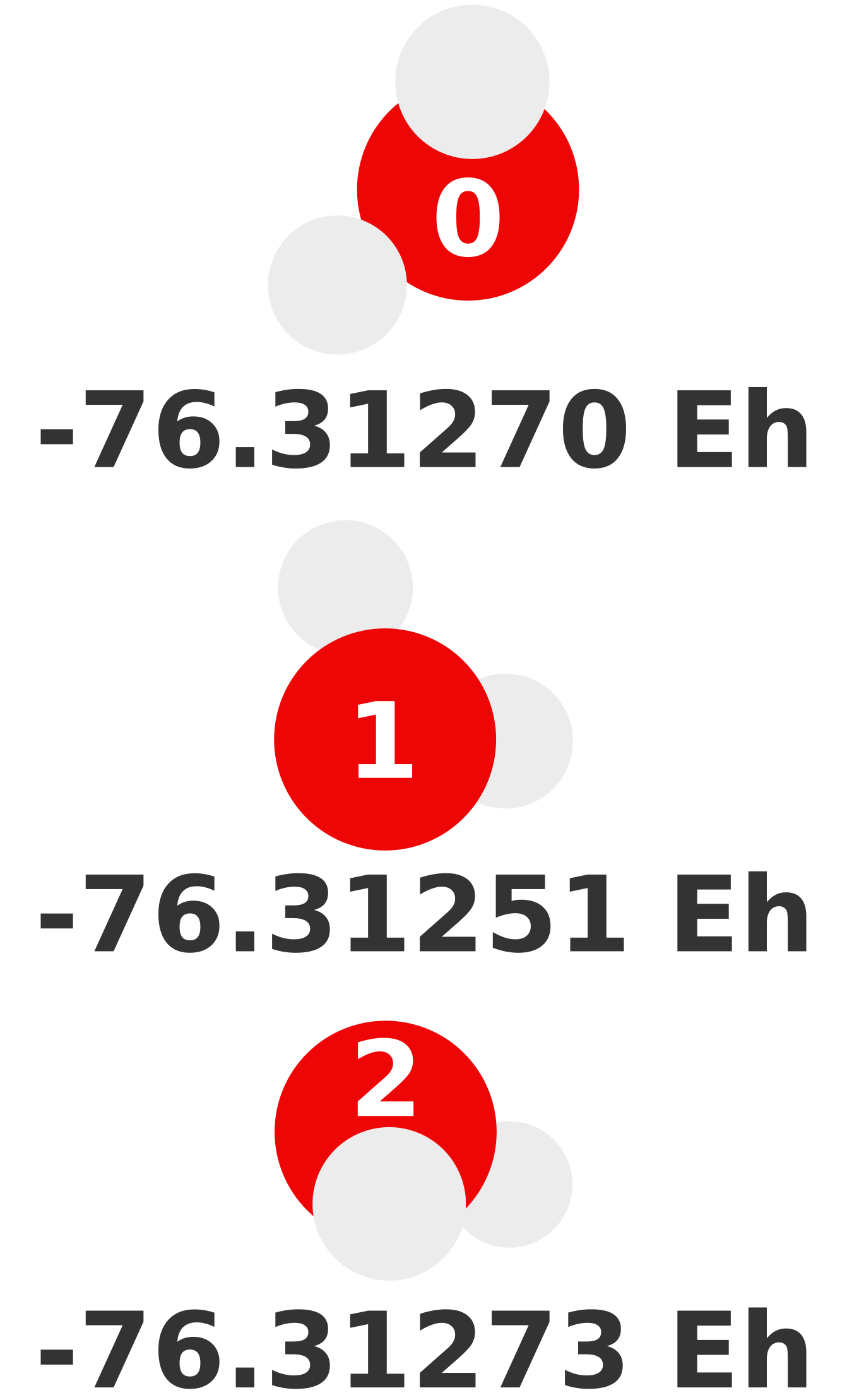
After computing \(E_0^{(1)}\), \(E_1^{(1)}\), and \(E_2^{(1)}\) our sum becomes

\[E^{(1)} = -76.31270 \;\text{Eh} + -76.31251 \;\text{Eh} + -76.31273 \;\text{Eh} = -228.93794 \;\text{Eh}.\]

-228.93794 Eh is our 1-body prediction of this particular trimer. In terms of accuracy, the error is a whopping -0.02504 Eh (-15.7 kcal/mol). This error is unsurprising as we have yet to account for how these water molecules interact.

2-body#

Our previous 1-body prediction was subpar with a somewhat larger error. We can substantially reduce this error by accounting for how monomers interact with each other (i.e., dimer interactions). These interactions are called the 2-body contributions to the MBE, which is defined in Equation (2). Essentially, we need to compute the total energy of each possible dimer and subtract out the monomer (i.e., lower order) contributions. Whatever energy is left over is the 2-body contribution of that dimer to the sum.

We visually depict these three 2-body calculations below.

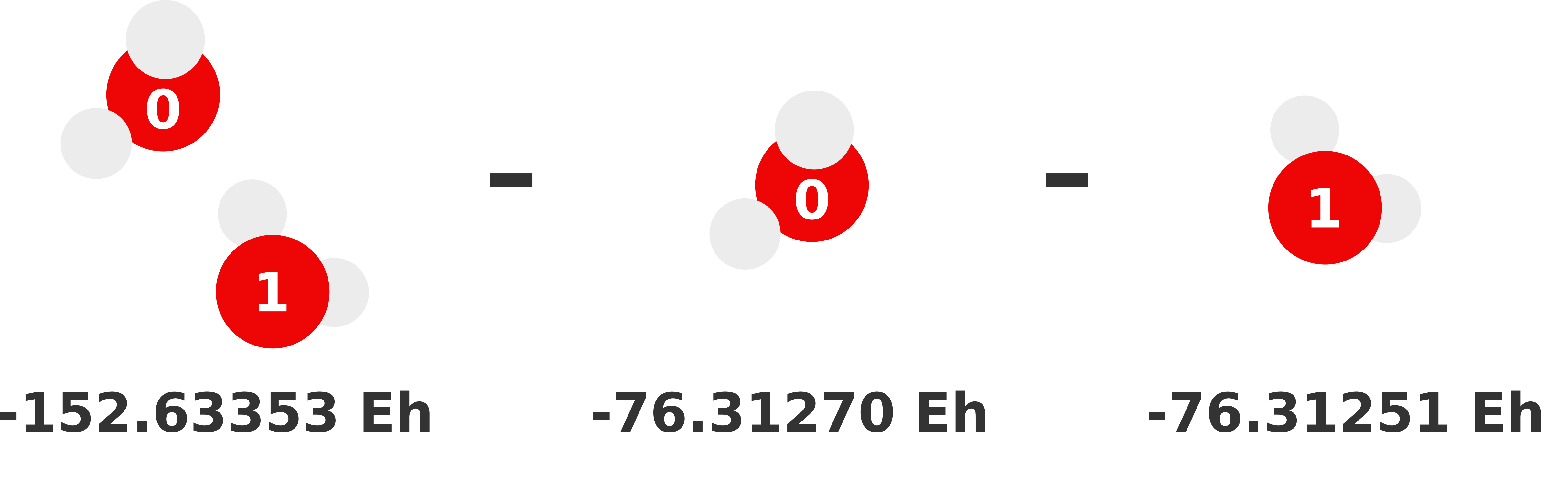
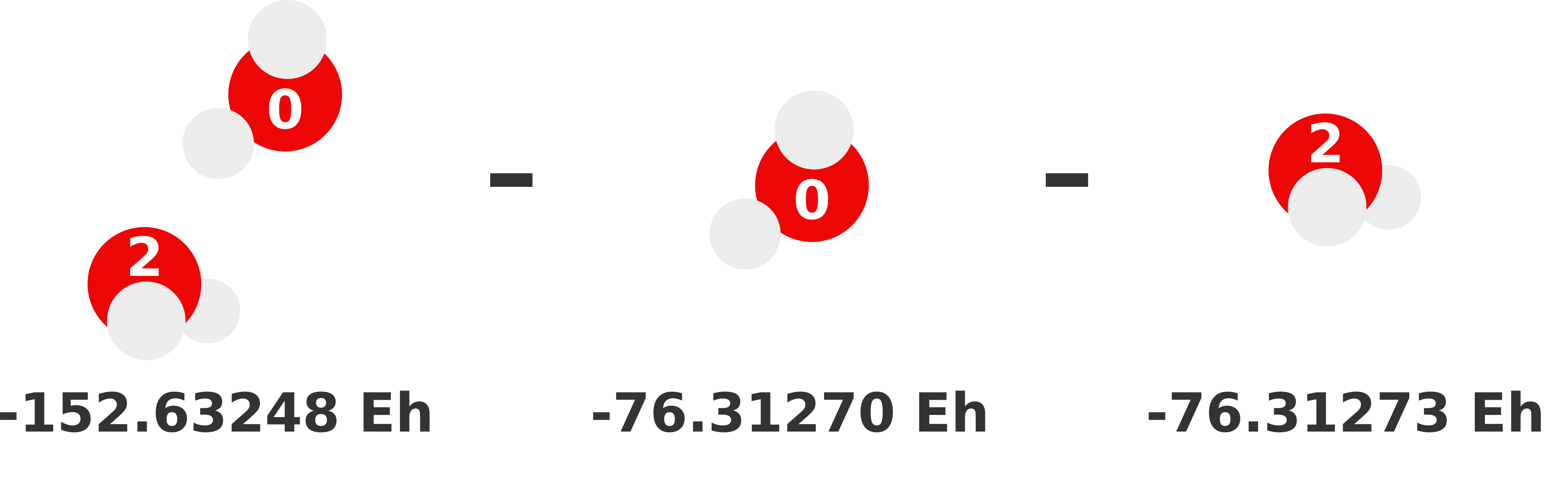
Note

We can reuse the monomer energies calculated in the previous section because our structure has not changed!

Our total 2-body term is just the sum of these 2-body contributions:

\[\Delta E^{(2)} = \Delta E_{0,1}^{(2)} + \Delta E_{0,2}^{(2)} + \Delta E_{1,2}^{(2)}.\]

For our particular system, this ends up being

\[\Delta E^{(2)} = -0.00831 \;\text{Eh} + -0.00705 \;\text{Eh} + -0.00700 \;\text{Eh} = -0.02236 \;\text{Eh}.\]

Thus, our 2-body prediction is the original 1-body plus the 2-body term,

\[E^{(2)} = -228.93794 \;\text{Eh} + -0.02236 \;\text{Eh} = -228.96033 \;\text{Eh}.\]

Our 2-body prediction of this trimer is -228.96033 Eh. We have reduced our error by an order of magnitude to -0.00267 Eh (-1.7 kcal/mol)!

Attention

This leftover -1.7 kcal/mol is the 3-body energy of this trimer. However, we can only know these errors by comparing them to the trimer’s energy. Practical applications of MBE involve structures we actually cannot compute.

No free lunch#

Up to this point, we have swept a few things under the rug about how accurate and valuable MBEs are. In the past, MBE was often referred to as a “free lunch,” where high-light ab initio results for large systems are easily attainable with minimal loss of accuracy. Contemporary research shows this is only partially true; some nuances influence MBE accuracy. We discuss a few main aspects here so you can judge if this approach will work for your systems.

Curse of dimensionality#

As previously mentioned, one of the crucial aspects of MBEs is system fragmentation. When the number of fragments of a system grows, the total number of \(n\)-body combinations explodes. The figure below shows the number of 1-, 2-, and 3-body structures with respect to system size.

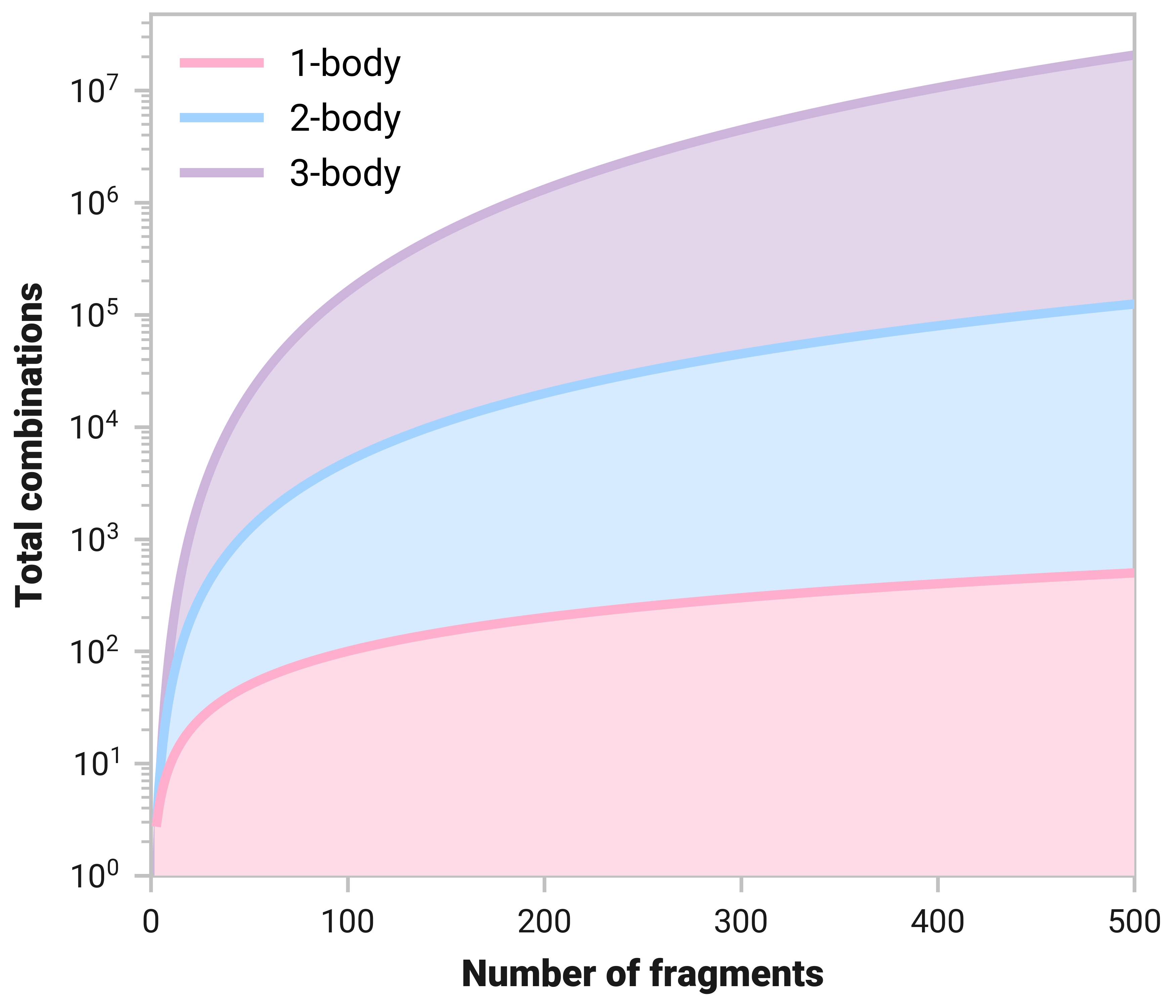
Large systems can quickly grow computationally cumbersome. For example, there are 161 700 total 3-body contributions for systems with 100 fragments.

Basis set errors#

TODO

Specifying fragments in mbGDML#

In order to make many-body predictions, we have to specify the fragments to generate \(n\)-body combinations. For example, we can make an MBE(2) prediction of a water and methanol cluster. This is rather small system, but it helps understand the concepts.

_images/2-body-example.png — Example structure of a water and methanol molecule.#

As with most atomistic modeling practices, we must specify atomic numbers and coordinates of the structure.

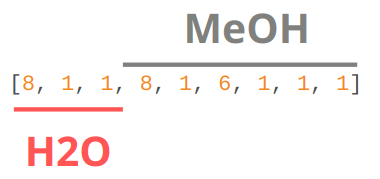
_images/2-body-z.png — `Z`: atomic numbers of all atoms in the system.#

_images/2-body-r.png — `R`: Cartesian coordinates in the same order as `Z`.#

Some ML potentials require the order of the atoms to be the same (e.g., GDML). This means any indistinguishable atoms must be in the same order. For the structure specified above, we must have the water molecule and then the methanol. Water’s oxygen atom must come before the hydrogens, whose order does not matter. With methanol, we specify the OH group first, then the CH3 group, where the first hydrogen is the one furthest from the OH hydrogen and proceeding in a clockwise direction.

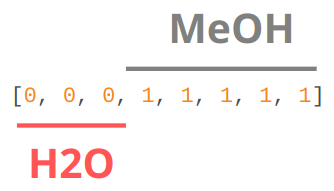
_images/2-body-entity-ids.png — `entity_ids`: integers that specify which fragment each atom belongs.#

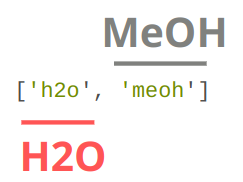
_images/2-body-comp-ids.png — `comp_ids`: labels for each `entity_id` used to determine relevant models.#

Obtaining many-body data#

Data sets used for training are briefly discussed here. Obtaining many-body energies and forces for these data sets generally requires the following multistep procedure.

Example

For illustrative purposes, we will provide examples for many-body GDML models for water (H2O), methanol (MeOH), and their mixtures.

Identify many-body interactions#

The many-body expansion requires many-body interactions between all possible species. Thus, we must have models for each possible comp_id combination. For a pure system, like water, this is just 1-, 2-, and 3-body models for the species. Multicomponent systems will have additional combinations that will require more models. Understanding your desired combinations will influence how to proceed with the following sections.

Example

Modeling water and methanol mixtures will require the following \(n\)-body interactions.

1-body: H2O MeOH
2-body: H2O+H2O H2O+MeOH MeOH+MeOH
3-body: H2O+H2O+H2O H2O+H2O+MeOH H2O+MeOH+MeOH MeOH+MeOH+MeOH

Generate relevant configurations#

Exhaustive conformational searches with flexible molecules is impossible to do analytically. Molecular dynamics simulations is a common technique to automatically sample structures. However, these simulations can become rather expensive depending on the method used to calculate energies and forces. Simulation quality is not too important; only realistic monomer, dimer, and trimer structures are needed at this stage. We often recommend using GFN2-xTB, a semiempirical quantum mechanics method, to efficiently run MD simulations at high temperatures.

Example

In the previous section, we note that multiple water and methanol structures are needed. Careful consideration is needed to minimize the number of simulations. For example, our ML models should apply to all concentrations. One possible simulation scheme could be two independent simulations:

one water molecule solvated by methanol,
and one methanol molecule solvated by water.

This will provide all necessary combinations of water and methanol molecules. The system must be large enough so the pure combinations (e.g., H2O+H2O and MeOH+MeOH) are not substantially affected by the other species.

Sample structures#

Once all simulations are done, \(n\)-body structures containing the desired number of components. The Python package reptar includes routines for sampling, but any procedure can be used.

All possible fragment \(n\)-body contributions need to be removed from each structure. Each sampled trimer requires energies and forces for the three unique dimers and monomers. Thus, we recommend a top-down approach where you sample all the desired trimer structures and then sample every possible dimer and monomer. This minimizes the total number of calculations required.

Example

Given our 3-body data sets, we would perform the following sampling from simulations.

Water in methanol (source)
- H2O+H2O+MeOH (destination)
- H2O+H2O+H2O (destination)
Methanol in water
- H2O+MeOH+MeOH
- MeOH+MeOH+MeOH
H2O+H2O+MeOH
- H2O+H2O
- H2O+MeOH
- H2O
- MeOH
H2O+H2O+H2O
- H2O+H2O
- H2O
H2O+MeOH+MeOH
- H2O+MeOH
- MeOH+MeOH
- H2O
- MeOH
MeOH+MeOH+MeOH
- MeOH+MeOH
- MeOH

Compute total energies and forces#

Energies and forces, preferable with a quantum chemical method needs to be computed for all sampled structures. This can be done in any way, but reptar has a driver and calculator for Psi4 if that is useful.

Compute many-body data#

Once we have total energies and forces of all monomers, dimers, and trimers we can begin to create many-body data sets. Note that instead of a top-down approach (i.e., trimer to monomers) we have to do bottom-up (i.e., monomers to trimers). For example, 2-body data—with monomer contributions already removed—are needed to compute 3-body data. Once this is done, you can train ML models on each \(n\)-body data set.

The following code shows a simple script to automatically compute many-body energies and forces using mbe_contrib() with reptar.

"""Compute n-body energies and gradients from total properties."""

import os
from mbgdml.mbe import mbe_contrib
import numpy as np
from reptar import File


rfile_path = './h2o.meoh-md-sampling.exdir'
parent_key = '/samples'

nbody_key = os.path.join(parent_key, 'h2o.2meoh')  # Data to make n-body
# Contains a nested list specifying the fragment key and if the data should be n-body.
fragment_keys = [
    (os.path.join(parent_key, 'h2o.meoh'), True),  # n-body data
    (os.path.join(parent_key, 'meoh.meoh'), True),  # n-body data
    (os.path.join(parent_key, 'h2o'), False),  # total data
    (os.path.join(parent_key, 'meoh'), False),  # total data
]

method = 'df.mp2.def2qzvppd'

energy_key = f'energy_ele_{method}'
energy_nbody_key = f'energy_ele_nbody_{method}'
grad_key = f'grads_{method}'
grad_nbody_key = f'grads_nbody_{method}'

use_ray = True
n_workers = 4

save = True  # If False, we just print the energies.




###   SCRIPT   ###

hartree2kcalmol = 627.5094737775374055927342256  # Psi4 constant
hartree2ev = 27.21138602  # Psi4 constant
ev2kcalmol = hartree2kcalmol/hartree2ev
kcalmol2ev = hartree2ev/hartree2kcalmol

# Ensures we execute from script directory (for relative paths).
os.chdir(os.path.dirname(os.path.realpath(__file__)))


def get_fragment_data(rfile, group_key, is_nbody):
    """Retrieve fragment (i.e., lower order) contributions.


    Parameters
    ----------
    rfile : :obj:`reptar.File`
        File to get data.
    group_key : :obj:`str`
        Key to group.
    is_nbody : :obj:`bool`
        If we should retrieve :math:`n`-body data or not.

    Returns
    -------
    Arguments for fragment (i.e., lower-order) data in :obj:`mbgdml.mbe.mbe_contrib`
    """
    global energy_key, energy_nbody_key, grad_key, grad_nbody_key

    if is_nbody:
        E = rfile.get(os.path.join(group_key, energy_nbody_key))
        G = rfile.get(os.path.join(group_key, grad_nbody_key))
    else:
        E = rfile.get(os.path.join(group_key, energy_key))
        G = rfile.get(os.path.join(group_key, grad_key))
    entity_ids = rfile.get(os.path.join(group_key, 'entity_ids'))
    r_prov_ids = rfile.get(os.path.join(group_key, 'r_prov_ids'))
    r_prov_specs = rfile.get(os.path.join(group_key, 'r_prov_specs'))

    return E, G, entity_ids, r_prov_ids, r_prov_specs


# Retrieve data
print('Loading data')
rfile = File(rfile_path, mode='a', allow_remove=False)

E_mb = rfile.get(os.path.join(nbody_key, energy_key), as_memmap=False)
G_mb = rfile.get(os.path.join(nbody_key, grad_key), as_memmap=False)
entity_ids = rfile.get(os.path.join(nbody_key, 'entity_ids'), as_memmap=False)
try:
    r_prov_ids = rfile.get(os.path.join(nbody_key, 'r_prov_ids'), as_memmap=False)
except RuntimeError as e:
    if 'does not exist' in str(e):
        print('Did not find r_prov_ids')
        r_prov_ids = None
try:
    r_prov_specs = rfile.get(os.path.join(nbody_key, 'r_prov_specs'), as_memmap=False)
except RuntimeError as e:
    if 'does not exist' in str(e):
        print('Did not find r_prov_specs')
        r_prov_specs = None

# Remove fragment energies and gradients
for fragment_key, is_nbody in fragment_keys:
    print(f'Removing {fragment_key} data')
    fragment_data = get_fragment_data(rfile, fragment_key, is_nbody)

    E_mb, G_mb = mbe_contrib(
        E_mb, G_mb, entity_ids, r_prov_ids, r_prov_specs,
        *fragment_data, operation='remove', use_ray=use_ray, n_workers=n_workers
    )


# Check if any are NaN
if np.count_nonzero(np.isnan(E_mb)) != 0:
    print('Check your calculations ... some are NaN')
    exit()

if save:
    # Put n-body data
    print(f'Saving n-body energies and gradients')
    rfile.put(os.path.join(nbody_key, energy_nbody_key), E_mb)
    rfile.put(os.path.join(nbody_key, grad_nbody_key), G_mb)

print('\n')
E_mb *= hartree2kcalmol
G_mb *= hartree2kcalmol
print('{:<10}   {:^10}      {:^10}    {:^10}'.format('Property', '   Min   ', '  Mean   ', '   Max   '))
print('{:<10}   {:^10}      {:^10}    {:^10}'.format('--------', '---------', '---------', '---------'))
print('{:<10}   {:^10.3f}      {:^10.3f}     {:^10.3f}'.format('Energy', np.min(E_mb), np.mean(E_mb), np.max(E_mb)))
print('{:<10}   {:^10.3f}      {:^10.3f}     {:^10.3f}'.format('Force', np.min(-G_mb), np.mean(-G_mb), np.max(-G_mb)))

Example

Perform the following computations with either total or \(n\)-body data. 1-body data is considered total here. Note that all of the unique entities should be contained in the lower-order data sets.

H2O+H2O (parent)
- H2O (fragment)
H2O+MeOH
- H2O
- MeOH
MeOH+MeOH
- MeOH
H2O+H2O+H2O
- H2O+H2O
- H2O
H2O+H2O+MeOH
- H2O+H2O
- H2O+MeOH
- H2O
- MeOH
H2O+MeOH+MeOH
- H2O+MeOH
- MeOH+MeOH
- H2O
- MeOH
MeOH+MeOH+MeOH
- MeOH+MeOH
- MeOH

Additional resources#

This is only a glimpse into the vast sea of MBE literature. Please see the following incomplete list of literature for additional information on many-body expansions.

Attention

If you have any questions or comments about the information presented here please do not hesitate to create a discussion on the GitHub repository.

Overview: 10.1063/1.5126216, 10.1063/1.4986110, 10.1063/1.4947087, 10.1063/1.4885846
Cutoffs: 10.1021/acs.jctc.9b01095
Molecular dynamics: 10.1021/acs.jctc.1c00780
Basis sets: 10.1021/acs.jctc.7b01232
Ions: 10.1039/D1CP00409C, 10.1021/acs.jctc.0c01309, 10.1021/acs.jctc.9b00749
Metals: 10.1063/5.0094598